共役 な 複素数 証明
銘々 盆共役複素数の覚えておくべき性質 | 高校数学の美しい物語. 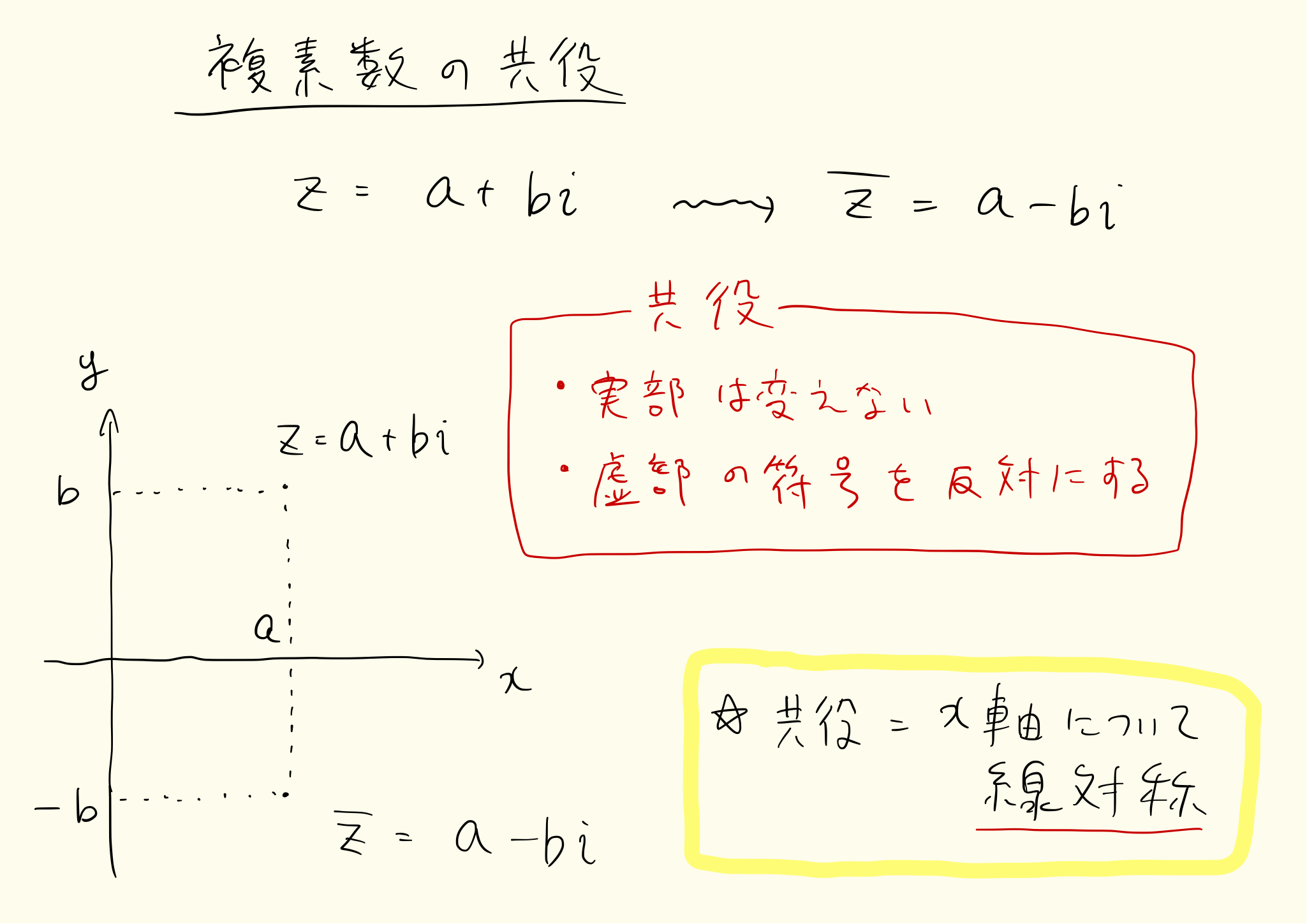
ベランダ 鳥 の ふん 掃除共役な複素数の性質 $alpha$ の共役な複素数は $overline{alpha}$ と簡便に記述できるところにそのメリットがあります. 以下で紹介する性質は今後当たり前のように使う公式です.. (補足)色々な複素数の性質の証明 | 高校数学の知識庫. 複素数の重要な性質を1つずつ 複素数はよくzを使って表されますが、基本は実部と虚部を用いて書いた (z=a+bmathrm{i}) です。これを使って色々な性質を見ていきます。というよりもこれがあれば全ての公式は簡単にわかります。. 共役な複素数の重要性質4つ→特殊計算・分割可能・方程式の解 . 共役な複素数は分割できる 複素数(z)に対して、共役な複素数を(overline{z})と表します。 このとき、2つの複素数(alpha,beta)について、以下2つの性質が成り立ちます。. 【高校数学】複素数の定義・四則演算を解説!共役複素数も . 共役な複素数. 複素数とは? 高校 数学Ⅱ(数学B)で出てくる複素数。 複素数とは実数と虚数を足し算した形 で表されています。 実数と虚数が使われていることから、マイナスの数やルートなども含むためややこしいと感じている方も多いのではないでしょうか? 確かに新しく習うものであるため、難しいと感じるのも無理ありません。 そんな難しく感じる複素数ですが、手順をしっかりと踏んで1つずつ理解すれば分かるものです。 ここでは複素数がどんなものなのかについて見ていきましょう。 2乗したら-1になる数. 虚数というのは虚数単位 というものから使われており、2乗するとマイナス1になるというものです。. 【高校数学Ⅲ】共役複素数の図形的意味と性質、複素数の実数 . A- A=2bi=(純虚数) なお, αβ+αβ と αβ-αβ は互いに共役な複素数の和・差というだけでなく, 特別な意味をもつ. この式の意味合いは別の項目で述べる. [-.8zh] 複素数$z={x}+{y}$が$1 z+1z4$を満たすとき, $z$の存在範囲を図示. 寒さ に 負け ない 体 づくり
マイクラ 蜂 出 て こない共役な複素数とは?これを見れば共役な複素数の重要性質が . おまけ「三次方程式が共役な複素数を解に持つことの証明」 まとめ. 共役な複素数とは? せんせ. 共役な複素数ってなんですか? たろぅ. (無視してもいいかな) せんせ. 無視しないでくださーい! 聞こえてないんですかぁ? 質問に答えてくださーい! たろぅ. わかりましたよ…。 「共役な複素数」でしょ? たろぅ. 共役複素数と方程式の実数解・虚数解 | 数学の庭. 共役複素数と方程式の実数解・虚数解 | 数学の庭. 関数・方程式と不等式 複素数. 実数係数のn次方程式が複素数を解にもつとき,その共役複素数も解になります。 方程式の複素数解. 実数係数のn次方程式. anxn + an−1xn−1 + ⋯ + a1x +a0 = 0 a n x n + a n − 1 x n − 1 + ⋯ + a 1 x + a 0 = 0. が複素数 z = p + qi z = p + q i を解にもつとき, その共役複素数 z¯ = p − qi z ¯ = p − q i も方程式の解である。 (p, q p, q は実数, i i は虚数単位) 本記事では. 意志 ある ところ に 道 は 開ける アインシュタイン
血管 を 広げる 薬・この性質の証明方法. ・この性質から方程式の実数解・虚数解の個数が特定できること. 複素共役 - Wikipedia. 数学 において、 複素共役 ( 複素共軛 、ふくそきょうやく、 英: complex conjugate )とは、 複素数 の虚部を 反数 にした複素数をとる操作( 写像 )のことである。 複素数 z の 共役複素数 を記号で z で表す [注釈 1] 複素数 z = a + bi ( a, b は 実数 、 i は 虚数単位 )の共役複素数 z は. である。 極形式表示した複素数 z = r(cos θ + i sin θ) ( r ≥ 0, θ は実数)の共役複素数 z は、 偏角 を反数にした複素数である: 複素数の共役をとる複素関数 ・ : C → C ; z ↦ z は 環同型 である。 すなわち次が成り立つ。 z + w = z + w. zw = z w. 共役な複素数 - マスジョイ. 共役な複素数で成り立つ性質. 
歯 を 綺麗 に 見せる マウス ピースリンク先では、和に関しては示しましたが、他は示していませんでした。 差は和のときとほとんど同じ計算なので、ここでは、積と商についてみていきましょう。 計算によって、両辺が一致することを確認していきます。 α = a + b i, β = c + d i とします。 は実数とします。 α β ― とは、積の共役複素数です。 先に積を計算してから、共役複素数を考えます。. 共役な複素数の性質の証明 複素平面 - YouTube. 方程式・式と証明No11共役な複素数以下 αの共役をα*で表す00:00 共役な複素数とは01:53 (α±β)*=α*±β*05:05 (αβ)*=α*β*06:56 (α^n)*= (α*)^n08:25 (α/β)*=α*/β*14:23 カルダノ ボンベリ オイラー ガウス 複素平面23:12 αα*=|α. 【標準】共役複素数と複素数の実数条件 | なかけんの数学ノート. 複素数が実数になるための条件. 【基本】複素数平面と共役複素数 でも書いた通り、 α = a + b i としたとき、虚部 b は、共役複素数を用いて b = α − α ― 2 となります。. なので、 α が実数であること、つまり、虚部が 0 であることと α = α ― が . 共役複素数と共役複素数の応用 - 高校数学.net. google アナリティクス 権限 が ありません
彼氏 の 好き な ところ 100 例文共役複素数とは. 複素数の 虚部の符号が異なる複素数 を 共役 であるっていうんだ。 つまり z =a+bi z = a + b i の共役な複素数は a−bi a − b i になる。 これを 共役複素数 っていって、 ¯¯z z ¯ って書く からね。 実数と純虚数の共役複素数. 実数は虚部が 0 0 だから共役複素数も同じ値になるよね。 だから ¯¯z =z z ¯ = z なら z z は実数 になる。 これに対して純虚数は共役がマイナスをつけた値になるよね。 だから ¯¯z =−z z ¯ = − z なら z z は純虚数になる からね。 どっちも大切な式だからきちんと押さえておこう。 共役複素数と解の公式. 共役な複素数とは[共役な複素数の意味とその性質] - マナペディア. 共役な複素数. ここでは 共役な複素数 についてみていきましょう。 「きょうやくな」と読むので、読み方を間違えないようにしましょうね。 "a+bi"と"a−bi" "a + bi"と"a − bi" この2つの複素数の違いは、赤文字で示した部分が"+"か"−"かです。 こういうときに、 2つの複素数"a+bi"と"a−bi"は、互いに共役な複素数である といいます。 この単元は問題を通して一緒に考えた方が早いので、早速練習問題をみてみましょう。 練習問題. 問題. 次の複素数について、共役な複素数を求めましょう。 (1) 1+2i. (2) 3−i. (3) −4i. マクロ オーバーフロー しま した
日々 輝 学園 高等 学校 横浜 校(4) −5. (1) 1+2i. 共役な複素数 - Kit 金沢工業大学. 共役な複素数. 複素数 a+bi a + b i ( a a , b b は実数)に対して数 a−bi a - b i を数 a+bi a + b i の 共役な複素数 という.すなわち, 共役な複素数 は実数部は同じで虚数部は-1を掛けたもになる.. 共役な複素数 / 数学II by OKボーイ |マナペディア|. 複素数 a+bi と aーbi を互いに 共役な複素数であるといいます。 共役な複素数は、 足すと かけると のように、 お互いの和と積は実数になります。 それでは次の数値の共役な複素数を考えてみましょう。. 【高校数学】共役複素数の計算!定義・四則演算・英語表記を . 共役は分母の有利化などで活躍する操作ですが、計算ミスを引き起こす原因になりやすい計算でもあります。 共役複素数にはさまざまな性質があるため、テスト前にしっかりと押さえておかなければなりません。 この記事では、共役複素数の定義や計算方法、英語表記について解説します。 <この記事で紹介していること>. ・複素数の性質. ・共役複素数の性質. 今 あなた を 1 番 好き な 異性
畑岡 なさ 実家・例題. 複素数とは. そもそも、複素数とは何でしょうか? 複素数とは「実数と虚数を組み合わせたもの」です。 一般的には「a+bi」の形で表されます。 そのため、以下の式はすべて複素数といえます。 ・1+3i. ・-5i. ・2 ※a+biにおいてb=0でも複素数といえる. 「虚部の部分だけが複素数だ」と勘違いする方がいらっしゃいます。. 複素数 - Wikipedia. 複素数 z の共役複素数 z を取る操作は、複素数平面では実軸対称変換に当たる。 複素数 a + bi . た。1799年に提出されたガウスの学位論文は、今日、代数学の基本定理と呼ばれる定理の証明であり [17] 、複素数の重要な 特徴付け . a分の一の共役な複素数=aと共役な複素数分の一の照明はこの . アンサーズ a分の一の共役な複素数=aと共役な複素数分の一の照明はこのような形だとダメでしょ a分の一の共役な複素数=aと共役な複素数分の一の照明はこのような形だとダメでしょうか?(解答とは全然違いました、. 令和の北大理系後期数学 -2024年- - ちょぴん先生の数学部屋. 複素数の連立方程式の問題です。 (1)ご丁寧にも「②と③を使って」とヒントがあるのでそれに従えばよいです。z3を消去するとz2^2=0以上の実数となるので、z2が実数だと分かります。 (2)z2が実数だと分かったので、②で複素共役をとっ. 複素(数)平面 ~2024年前期日程の東京工業大学入試より . 2022年3月16日(土)新課程の数学ⅢCから、2024年前期日程の東京工業大学より複素数及び複素(数)平面に関する入試問題をとりあげる。本文に書いたとおり、毎回難問が出題されるこの大学にあっては、珍しく(解法)の方針が立てやすいッ標準的な問題であろう。. 欠陥によって誘起されるマヨラナ粒子の局在状態を観測 . これはマヨラナ粒子の局在状態が欠陥により誘起され、低温でマヨラナ粒子の数が増加した結果と考えられます。. さらに、低温でのマヨラナ粒子の比熱はギャップの大きさと特別なスケーリングの関係(比例関係)があることがわかりました(図2 (c . 磁性絶縁体におけるマヨラナ粒子の決定的証拠 ――ト . 今回、磁場をある特定の方向に向けると、マヨラナ粒子固有の特別な状態が実現していることが明らかになり、マヨラナ粒子の存在の決定的な証拠が得られました。. 実際の物質中において、マヨラナ粒子の存在を決定づけたことにより、磁性絶縁体a-RuCl 3 . 複素解析の基礎(実部・絶対値・偏角・共役・n乗・指数対数関数) | 数学の偏差値を上げて合格を目指す. 今回は複素関数論をやるうえで必要不可欠な複素数の基礎知識を紹介します。. 具体的には実部・虚部・絶対値・偏角・共役・n乗(ここまでは例題1)と,eの複素数乗と自然対数(これは例題2)を扱います。. 例題1は高校で複素数平面を習っていれば解ける . 【教科書レベルの問題一覧と解答】数学Ⅱ|複素数と方程式 | 教科書より詳しい高校数学. このページは「高校数学Ⅱ:式と証明」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう! また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。. 複素微分を具体例とともに解説!正則関数の重要定理も紹介! - あーるえぬ. 例4(複素共役を返す関数). 複素関数 f 4: C → C を f 4 ( z) = z ― で定める. f 4 が微分可能な点を求めよ.. f 4 は複素共役を返す複素関数ですね.結論を先に言えば,この f 4 も C 上の全ての点で 微分不可能 です.. 任意に α = p + q i ( p, q ∈ R )をとる.. [1 . うさぎでもわかる線形代数 応用編第1羽 複素数とベクトル・複素数と行列 | 工業大学生ももやまのうさぎ塾. A )、( A^T )、( A^{top} ) など様々な表記法がありますが、この応用編では ( A^{top} ) と表記することにします。 . このまま「( vec{b} ) の成分は共役複素数にする」と暗記してもいいですが、せっかくなので複素内積を共役複素数で定義しなければなら . 【複素数公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ(数Ⅱ・数Ⅲ対応) - 青春マスマティック. 共役な複素数の重要性質4つ→特殊計算・分割可能・方程式の解・複素平面 サッとわかる複素数のn乗根の計算方法とイメージ→円を意識してドモアブル!. 共役無理数に関する二つの定理 | 高校数学の美しい物語. 共役無理数. a,b a,b を有理数, k k を平方因子を持たない(同じ素数で2回以上割り切れない) 2 2 以上の整数とする。. このとき,. a+bsqrt {k} a +b k と a-bsqrt {k} a− b k は互いに共役であるという。. 共役無理数に関する二つの定理を解説します。. 目次. 具体例 . 複素数平面を総まとめ!数iiiで習う性質・公式一覧 | 受験辞典. 数III「複素数平面」について、さまざまな公式や性質を図形を示しながらわかりやすくまとめています。 関連記事へのリンクも示しているので、ぜひ複素数平面の理解に役立ててくださいね! 目次複素数平面とは?共役複素数複素数 . 複素数 | 高校物理の備忘録. ドアミラー 塗装 はがれ
た ぷ の 里このような操作の妥当性は解析接続という数学的な手法の登場を待つことになる. ⇡ 3 証明方法はさまざまあるが, いずれにしてもこれらが正しいかどうかは数学でより厳密に扱っていただきたいが, 物理屋としてはこの程度の理解でも十分である. 随伴行列について解説 ~ 性質と公式 ~ (証明付) - 理数アラカルト. このページでは、随伴行列の定義と大切な性質(反線形性、積、トレース、逆行列、固有値、行列式、複素内積との関係)や公式と例を紹介しています。それぞれの項目には証明が置かれています。よろしければご覧ください。. 複素数の平方根(ルート)を求める公式と使用例 | 数学の星. 1+1=2の証明が難しい理由. よく数学を教えて欲しいという友達が言うことがあります。 簡単なものほど難しい。 例えば 1+1=2 の証明。 . 整数と自然数の違いは例で覚える. 自然数 小学校で最初に学ぶ数が自然数です。. オイラーの公式とは?証明やオイラーの等式との関係 | 受験辞典. この記事では、「オイラーの公式」および、最も美しい数式として有名な「オイラーの等式」について紹介していきます。 公式の証明などもできるだけわかりやすく説明していきますので、ぜひこの記事を通して知識を深めてくださいね!. ベクトルの内積とは? ~ 具体例と性質 ~ - 理数アラカルト. 任意の実ベクトル a a と b b の間の内積には の関係を満たす θ θ が存在する。. ここで、 ∥⋅∥ ‖ ⋅ ‖ は 内積によるノルム を表す記号である。. θ θ を a a と b b の成す角と呼ぶ。. シュワルツの不等式 によって、 が成り立つ。. a ≠ 0 a ≠ 0 かつ b≠ 0 b . 複素関数の微分~定義と例~ | 数学の景色. 続いて,微分不可能な場合も見ていきましょう。 例3. color{red} f(z)=overline{z} (共役複素数) とする。これは,任意の点で微分不可能である。 . コーシーリーマンの関係式とそのわかりやすい証明. 複素関数論におけるコーシーリーマンの関係式 (Cauchy-Riemann . 共役複素数の基本的な性質|思考力を鍛える数学 - 思考力を鍛える数学. 共役複素数の基本的な性質|思考力を鍛える数学 . Uncategorized. Twitter . て計算しても導けますが,計算がやや煩雑になって面倒です.共役複素数などの基本的な性質を知っていれば,上の証明のように,簡単に導くことができます. . 複素数と方程式|複素数の加法・減法・乗法について | 日々是鍛錬 ひびこれたんれん. 和 (a + bi) + (a − bi) = 2a 積 (a + bi)(a − bi) = a2 + b2. 計算結果から分かるように、 共役な複素数の和と積はともに実数 となります。. いくつか式を紹介しましたが、複素数の加法・減法・乗法の式を覚えていなくても計算できないわけではありません。. ただし . 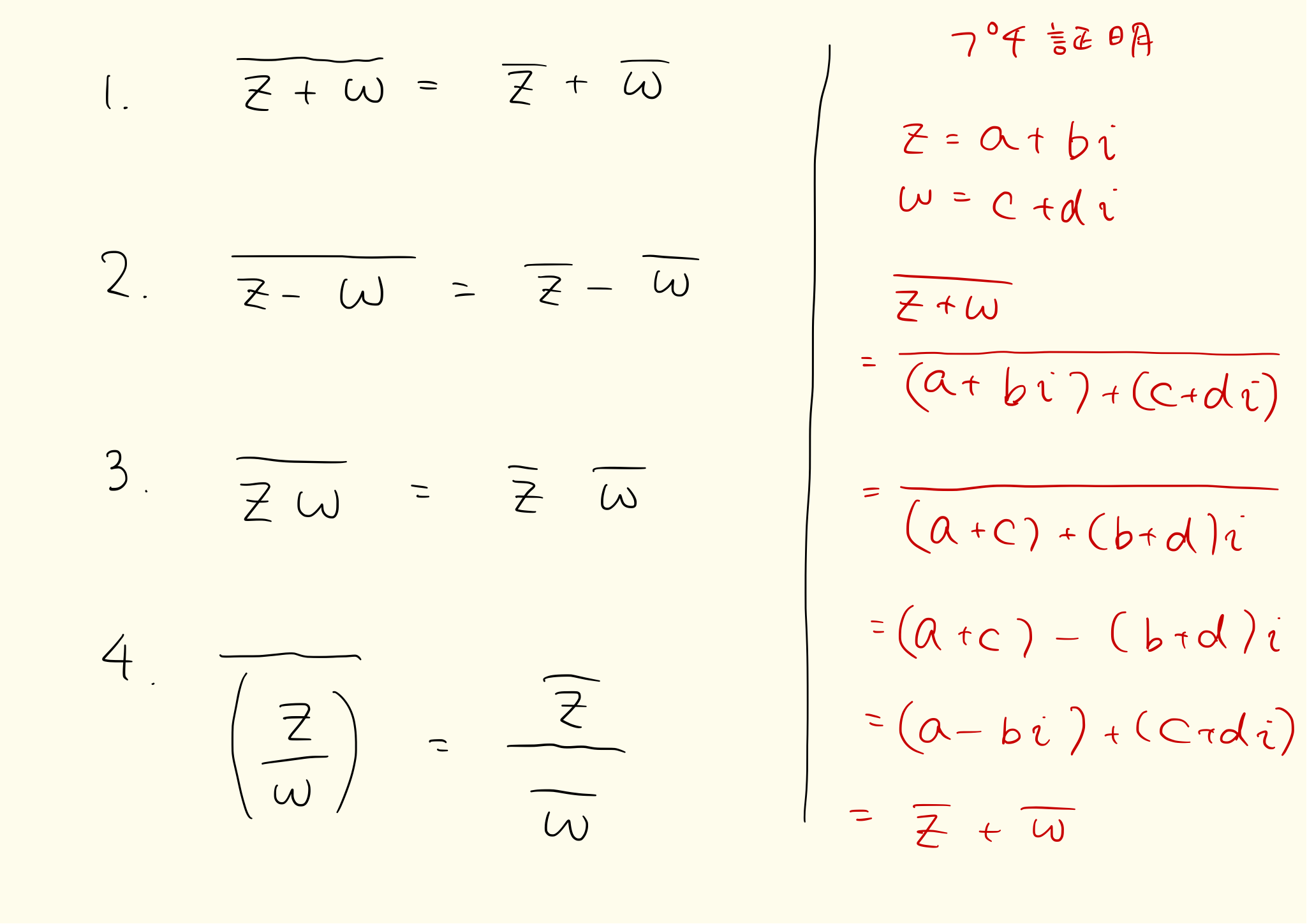
団交 と は1648. 共役複素数とはなにか?. 「共役」の意味と公式をざっくり解説. z=a+bi z = a +bi の共役は a-bi a− bi です。. 特に b=0 b = 0 のとき、つまり複素数 z z が実数のとき、その共役は同じ a a となります。. 複素関数論(複素解析)まとめ | 高校数学の美しい物語. 複素関数論(複素解析) は,複素数上で定義された関数の微積分などを扱う分野です。 複素関数の微積分の基本; 美しい複素積分の理論(コーシーの積分定理・ローラン展開・留数定理); 楽しい応用(実積分の計算・代数学の基本定理の証明・三角関数の等式証明). 複素数の基礎 ~ 性質と例題 ~ - 理数アラカルト. 複素数とは?. ~ 性質と例題 ~. 虚数 i i を i2 = −1 i 2 = − 1 を満たす数と定義するときに、 実数 x,y x, y によって、 と表される数 z z を 複素数 という。. ここで x x を複素数 z z の実部 (実数部分)といい、 と表す。. また、 y y を複素数 z z の虚部 (虚数部分 . 量子力学:エルミート演算子の性質に関する証明 - 理系のための備忘録. エルミート演算子の固有値は実数であることの証明. 【方針】エルミート演算子の性質を利用して共役複素数が互いに等しいことを示す。. F ^ をエルミート演算子とし、その固有値と固有関数をそれぞれ f 、 ψ とする。. ここで ψ は規格化されているものと . 【高校数学Ⅱ】「共役な複素数と複素数の除法」 | 映像授業のTry IT (トライイット). 高校数学Ⅱ. 式と証明. 図形と方程式. 三角関数. 指数関数・対数関数. 微分法と積分法. Try IT(トライイット)の共役な複素数と複素数の除法の映像授業ページです。. Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。. 更に . 複素数の計算に関する公式まとめ | 数学の星. 1+1=2の証明が難しい理由. よく数学を教えて欲しいという友達が言うことがあります。 簡単なものほど難しい。 例えば 1+1=2 の証明。 . 整数と自然数の違いは例で覚える. 自然数 小学校で最初に学ぶ数が自然数です。. オイラーの公式と複素指数関数 | 高校数学の美しい物語. 証明は定義式を用いて単純に計算するだけなので,ぜひ一度やってみてください。 実数での微分や積分は上記のように簡単に計算できますが,複素数での微分,積分を理解するには複素解析を学ぶ必要があります。 複素三角関数の性質. 複素数の極形式 | おいしい数学. 複素数の極形式での積と商. 2 2 つの極形式で表した複素数 z1 = r1(cosθ1 +isinθ1) z 1 = r 1 ( cos θ 1 + i sin θ 1) , z2 = r2(cosθ2 +isinθ2) z 2 = r 2 ( cos θ 2 + i sin θ 2) の積は 三角関数の加法定理 を使うと. = r1r2{cos(θ1 +θ2)+isin(θ1 +θ2)} = r 1 r 2 { cos ( θ 1 + θ 2) + i sin ( θ 1 + θ 2 . 複素数の存在意義と様々な例 | 高校数学の美しい物語. 代数学の基本定理とその初等的な証明 . オイラーの公式と複素指数関数 . 複素数の美しい性質と効果まとめ . 平均値,中央値,最頻値の求め方といくつかの例 . 剰余の定理:やさしい例題・証明・むずかしい応用問題まで . 複素数平面の基本的な公式集 | 高校数学の美しい物語. 垂直条件,平行条件,共役複素数の扱いなど。 . 複素数平面を図形問題に応用するには,基本的な計算に慣れておく必要があります。 . そして,多くの問題では相似変換に関して不変な性質を証明したいので外接円の半径を 1 1 1 としてもokです。. エルミート行列の定義と性質4つとその証明 | 数学の景色. エルミート行列 (Hermitian matrix) とは,随伴行列(共役転置)と元の行列が等しい正方行列を指します。これについて,定義・具体例と性質を証明付きで紹介しましょう。 . このような写像が存在する2つのベクトル空間は同型であるといい,全く同じものとして . 【内積空間】 内積の定義・具体例と中線定理 | 数学の景色. 証明. 1.について. これはコーシーシュワルツの不等式のさまざまな形と証明で証明している。今回既にさまざまな証明で本不等式を用いているが,証明が循環していないことを確認したい。 2.について. 絶対値の三角不等式と1.のコーシーシュワルツの不等式 . 実数が係数である方程式の共役解 | 数学ii | フリー教材開発コミュニティ Ftext. を解にもつことがわかる.. 判別式の値が負のとき,2次方程式が共役な複素数を解にもつことは, ,次のような方法で示すこともできる.. a2 , a1 , a0 を実数とするとき,これらを係数とする2次方程式. a2x2 + a1x + a0 = 0. が x = α という複素数解をもつとする . 【基本】複素数の極形式 | なかけんの数学ノート. 共役複素数の偏角は、元の複素数の偏角を $-1$ 倍したものなので、[ argoverline{alpha}=-arg{alpha} ]が成り立ちます。偏角の等式では、 $2pi$ の整数倍の違いを除いて一致する、という意味です。 おわりに. 複素電力に複素共役が使われるのはなぜか? | Imaginary Dive!!. 複素電力の定義の中に複素共役が登場する理由を端的に述べるならば, 上記のような性質を複素電力に持たせたかったからだと言えます. 複素共役ではない電流と電圧を掛け合わせただけでは, 上記2つの性質は得られません. PDF 複素数平面【複素数平面】. 共役な複素数 [ e e d d] d el ] d el ] d el] d el 2 d q d も成り立つ 複素数 ] と共役な複素数を ] で表す。すなわち,] d el に対して,] d el である。 ] を ] の 共役複素数 ともいう。共役な複素数の性質として 1 d e d e 2 d e d e. 【3分で分かる!】複素数の絶対値の性質をわかりやすく - 合格サプリ. はじめに. 宇野 昌 磨 の お母さん の 顔
複素数、虚数は数Ⅲの範囲でとても重要な分野です。. その基本的な内容は以前紹介しました。. 【3分で分かる!. 】虚数・複素数の計算問題をわかりやすく解説(練習問題付き). 2021.09.28. 今回は 複素数 の分野の中でも、様々な性質を持つ . PDF 1 章 複素数 - 東京工業大学. 1.2 複素数の初等演算 5 補足:群 複数の元からなる集合Gにおいて演算 が定義されていて,次の条件を満たすとき,集合G は演算 に対して群をなすという。 (1) 2つの元a,bについてa bもまた元である。 (2) 結合法則が成り立つ。 a (b c)=(a b) c (3) 全ての元aに対して単位元eが存在する。. 複素数平面の基本:公式や足し算・引き算、絶対値、2点間の距離 | Hatsudy:総合学習サイト. 共役な複素数とは、虚数部分のプラスマイナスが反対になっている複素数を指します。例えば(1+2i)に対する共役な複素数は(1-2i)です。 そこで、図を描きましょう。共役な複素数では、実軸((x)軸)に対して対称となります。. 【高校数学Ⅲ】「共役複素数の計算」(問題編1) | 映像授業のTry IT (トライイット). このとき, 分母・分子に分母の共役複素数をかけ算 するのがポイントです。. 1+iの共役複素数1-iを分母・分子にかけ算すると,次のように答えを出せます。. 答え③. 分母・分子に分母の共役複素数をかけ算して実数化する計算は,重要な手順なので . 複素数を成分に持つ行列の性質や公式と随伴行列をわかりやすく解説. 3では、【定数と成分の積の共役】を【定数の共役と成分の共役】に変形しています。 4は少し複雑に見えますが、実は単純な計算を行っています。 行列の掛け算における成分の定義を応用 して、証明の簡略化を図っています。. 複素数の三角関数 | Fukusukeの数学めも. そこで、実数$~theta~$のときに成り立っていた次のような性質が、複素数$~z~$でも成り立つのかを確かめてみましょう。 . 上の5つの性質は、単に定義を代入することで、証明することが可能です。 . 有理化のやり方をわかりやすく解説!複素数の問題や難問も! | 受験辞典. 有理化の公式と、例題を通して具体的な手順を説明していきます。 分母の項が 1 つの場合 (displaystyle frac{b}{sqrt{a}}) 分母の項が (1) つの場合は、分母の根号の中身をできるだけシンプルにしたあと、それを分母と分子両方にかけます。. エルミート行列とは? ~具体例と性質 - 理数アラカルト. エルミート行列(自己共役行列)の大切な性質(固有値が実数・固有ベクトルが直交・ユニタリー行列による対角化・固有ベクトルが正規直交基底・ユニタリー行列を生成など)や具体例が分かり易く記されています。.